Codes de calculs industriels

Présentation générale

Descriptif de l’enseignement

Utilisation de logiciels de simulation éléments-finis pour la mécanique (eg. Abaqus, Ansys, Cast3m, Salome-Meca, Comsol, etc). On utilisera principalement les interfaces graphiques des différents logiciels mais on commencera aussi à apprendre langages de script pour la mise en donnée et le post-traitement : Python, Gibiane, etc.

1. Initiation

•  Modules usuels pour la définition d’un calcul élastique (choix de la géométrie, du modèle, du matériau, de la discrétisation
  spatiale/temporelle).
• Réalisation d’assemblages.
• Partitionnement du domaine.
• Post-traitement : affichage de champ, tracé de courbes.

2. Utilisation avancée

• Poutres : Solides élancés en traction, flexion, torsion avec modèles de Bernoulli et Timoshenko. Treillis.
•  Plaques : Solides minces avec modèles de Kirchhoff-Love et Reissner-Mindlin.
• Plasticité : Plasticité parfaite. Modèle de Prandtl-Reuss.
• Contact : Avec ou sans frottement. Méthode de pénalisation ou avec multiplicateur de Lagrange. Notion de maillage
  compatible.
• Matériaux composites : Conditions aux limites périodiques.
• Dynamique : Implicite, explicite.
• Vibrations : Fréquences propres, modes propres.
• Thermique et thermomécanique : Conduction thermique, dilatation thermique.

Pré-requis

Bases de la méthode des éléments-finis.

Objectifs

Au terme de cet enseignement, l’étudiant devra savoir :

• Maîtriser les outils de création géométrique : esquisse, contraintes, cotes, symétrie, extrusion- révolution, etc.
• Connaître les propriétés des différents éléments-finis (compatibilité, degrés de liberté, méthode d’intégration, fonctions de
  forme, convergence).
• Choisir les éléments appropriés 3D, plaque, ou poutre afin d’éviter les problèmes classiques (verrouillage, mode à énergie
  nulle).
• Raffinement les maillages pour optimiser le temps de calcul et la convergence.
• Simuler des problèmes non-linéaires faisant intervenir de contact, la plasticité, la rupture, etc, en quasi-statique ou en dynamique.
• S’informer en utilisant la documentation des logiciels.
• Effectuer la mise en donnée ainsi que le post-traitement en se basant sur l’interface graphique ou un langage de script.

Détail des séances

Initiation (5 séances)

Séance 1 : Présentation générale d’Abaqus

Séance 2 : Modes Part et Property Module Part :

• Outil de création d’esquisse (Sketch)
• Esquisse sous-contrainte et sur contrainte.
• Création de géométries simples : rectangles-cercles.
• Réalisation d’une coupe pour obtenir un elèvement de matière.
• Création de traits de construction.
• Ajout de cotes.
• Outil ligne brisée.
• Ajout automatique de contraintes (angle droit).
• Fichier rpy.
• Module Sketch.

Module Property :

• Outil de création d’un comportement et manager.
• Outil de création d’une section et manager.
• Outil d’assignation d’une section à une géométrie.

Mécanique / Eléments finis:

• Loi sigma-epsilon, limite d’élasticité, écouissage isotrope/cinématique, plasticité parfaite.
• Notion de raffinement du maillage dans les zones de fort gradient.
• Résistance des matériau et nécessité de définition une section.

Module Property :

• Outil d’assignation d’une orientation du matériau.
• Partitionnement de la géométrie.
• Création de de matériaux assignés chacun à une partie de la géométrie.

Exercice applicatif : diffusion de la chaleur dans un pavé.

Poutres (4 séances)

Dans cette partie du cours constituée de 4 séances de Travaux Pratiques, on apprend à utiliser différences méthodes permettant d’utiliser la théorie des poutres dans Abaqus. La théorie des poutres en traction, en flexion et en torsion le cours Poutres et Plaques du Master 1 SGM est supposée être connue des étudiants. Bien qu’il s’agisse d’une théorie approchée, la théorie des poutres est largement utilisée pour les calcul numériques industriels car elle permet de réduire drastiquement la densité des maillage dans le cas d’un solide élancé, par exemple un renfort métallique dans un bloc de béton armé.

Il existe différents types d’éléments-finis basés sur la théorie des poutres disponibles dans Abaqus, notamment les éléments te type Truss, Beam, et Spring seront utilisés. On apprendra dans quelle circonstance utiliser un élément plutôt qu’un autre. Quatre séances de TP de 3h seront consacrées à l’étude des poutres. Les séances 1 et 2 sont basées sur l’étude des poutres en traction-compression, la séance 3 et 4 permettent d’étudier plus en détail la flexion et la torsion.

TP1 : Poutres en traction Dans le 1e TP on étudie un système composé de 2 poutres articulées en un point M. Ces 2 poutres sont sollicitées en compression sous l’effet du point du point M.

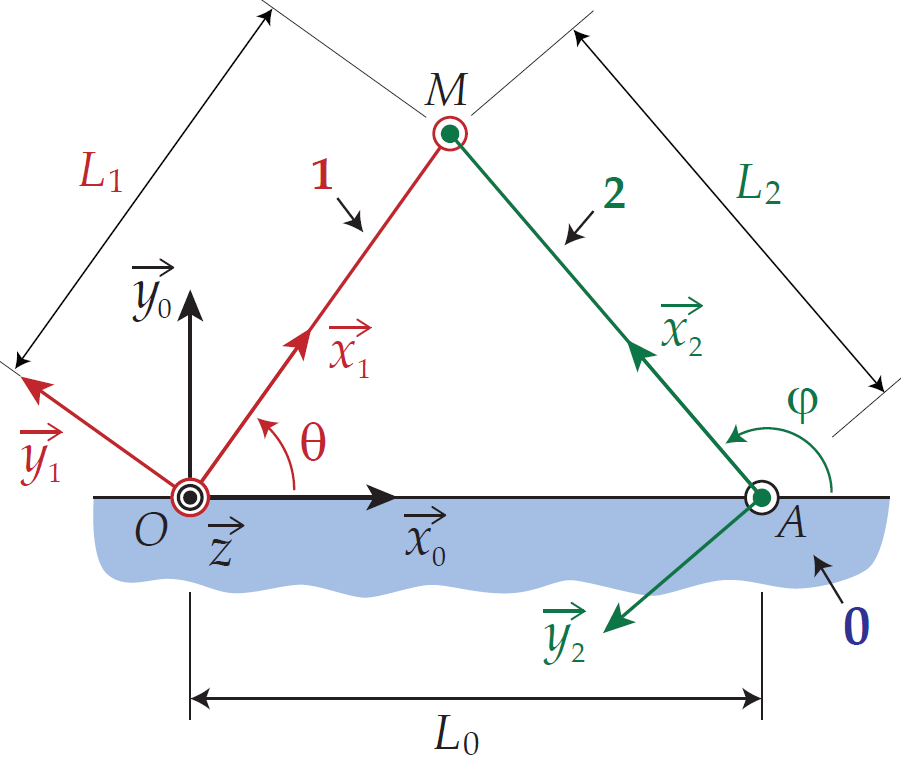Ce problème a la particularité qu’il peut être résolu dans Abaqus en utilisant aussi bien des éléments Truss, que Beam, ou Spring :

• Dans le cas des éléments Truss, une seule esquisse suffit à définir les deux poutres et les articulations aux points O, A, et M sont définies implicitement.
• Dans le cas des éléments Beam, il faudra définir une esquisse pour chaque barre. L’assemblage permettra ensuite de positionner les barres et une articulation sera ajoutée entre les deux barres. Comparativement aux éléments Truss (et à beaucoup d’autres élements dans Abaqus), les éléments Beam ont la particularité de posséder non seulement des degrés de liberté en translation mais aussi des degrés de liberté en rotation. Cette complexité supplémentaire permet à ces éléments de simuler des déformations de flexion et de torsion, même si cette fonctionnalité n’est pas utilisée dans ce premier TP.
• Finalement les éléments Spring permettent de définir des éléments-finis en traction-compression comme des ressorts. Contrairement aux éléments Truss ces éléments ne sont pas basés sur la définition d’un matériau avec un module d’Young E et d’une section pour la poutre S, mais sur la définition de la constante de raideur K.

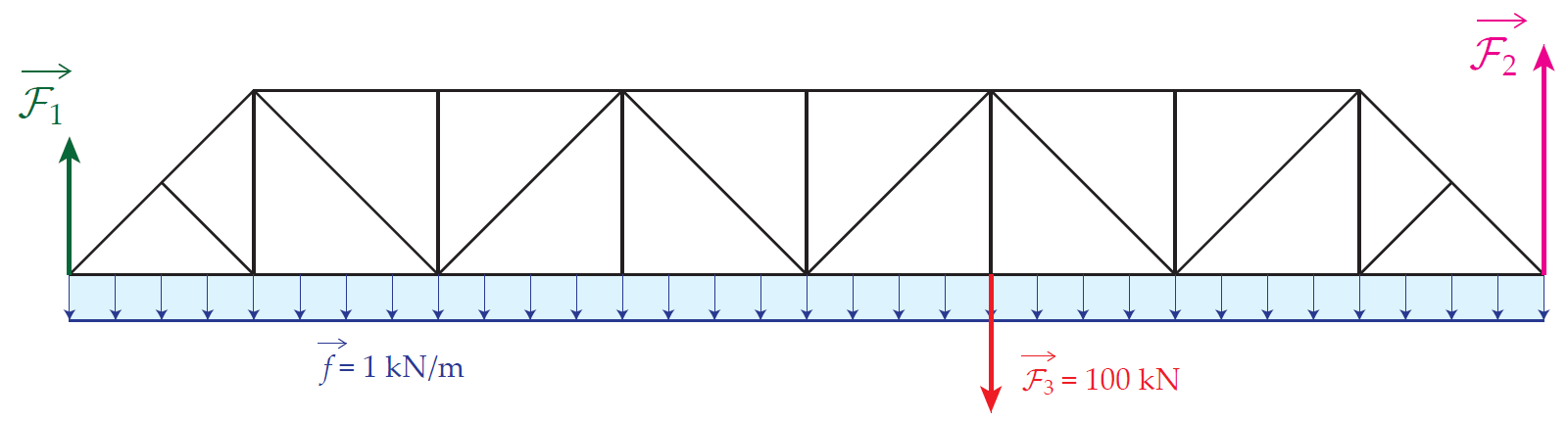
TP2 : Treillis La 2e séance de Travaux Pratiques permet d’étudier plus particulièrement la notion de treillis, c’est à dire un assemblage composé d’un nombre important de poutres.

Si ces poutres sont articulées avec des liaisons pivot, la manière la plus simple de les modéliser est d’utiliser des éléments Truss car toutes les poutres pourront être définies dans la même esquisse. Des outils de duplication des traits pourront être utilisés pour simplifier la création de l’esquisse contenant de nombreux traits.

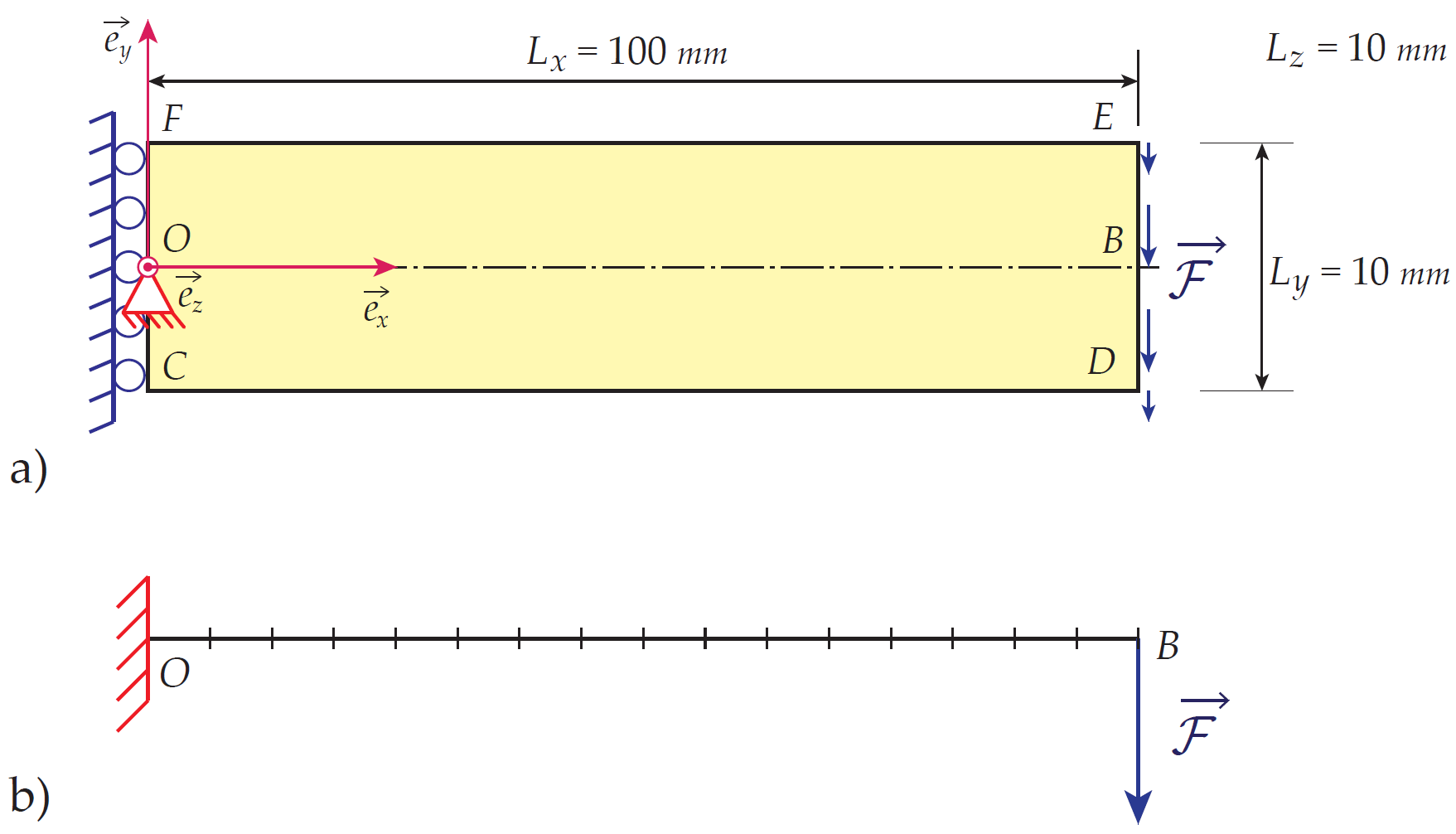
TP3 : Flexion La 3e séance de Travaux Pratiques est basées sur l’étude d’une poutre en porte-à-faux encastrée sur son côté gauche et sollicitée en flexion par des efforts verticaux appliqués sur son côté droit.

Deux modélisations différentes seront utilisées pour cette séance de TP :

• Une modélisation bidimensionnelle basée sur la mécanique des milieux continus en petite déformations. Il est a noté qu’une solution théorique de ce problème est connue et peut être trouvée dans [Timoshenko et Goodier, 1951]. Dans Abaqus, on se basera sur l’utilisation d’éléments linéaires de formes triangulaires.
• Une modélisation unidimensionnelle pouvant être basée sur la théorie de Timoshenko ou sur la théorie de Bernoulli. Dans la cas 1D, les solutions analytiques basées sur la théorie de Timoshenko et de Bernoulli sont également connues. Les calculs numériques réalisés dans Abaqus seront réalisés en utilisant des éléments Beam basés sur la théorie de Timoshenko d’une part et sur la théorie de Bernoulli d’autre part.

La séance de TP permettra de tracer les 3 solutions analytiques de la déformée basées sur les 3 théories (MMC, Timoshenko, Bernoulli) dans un tableur. Ensuite les 3 solutions numériques basées sur les 3 différentes théories seront tracées. Finalement, les erreurs seront tracées en prenant comme référence la solution analytique bidimensionnelle.

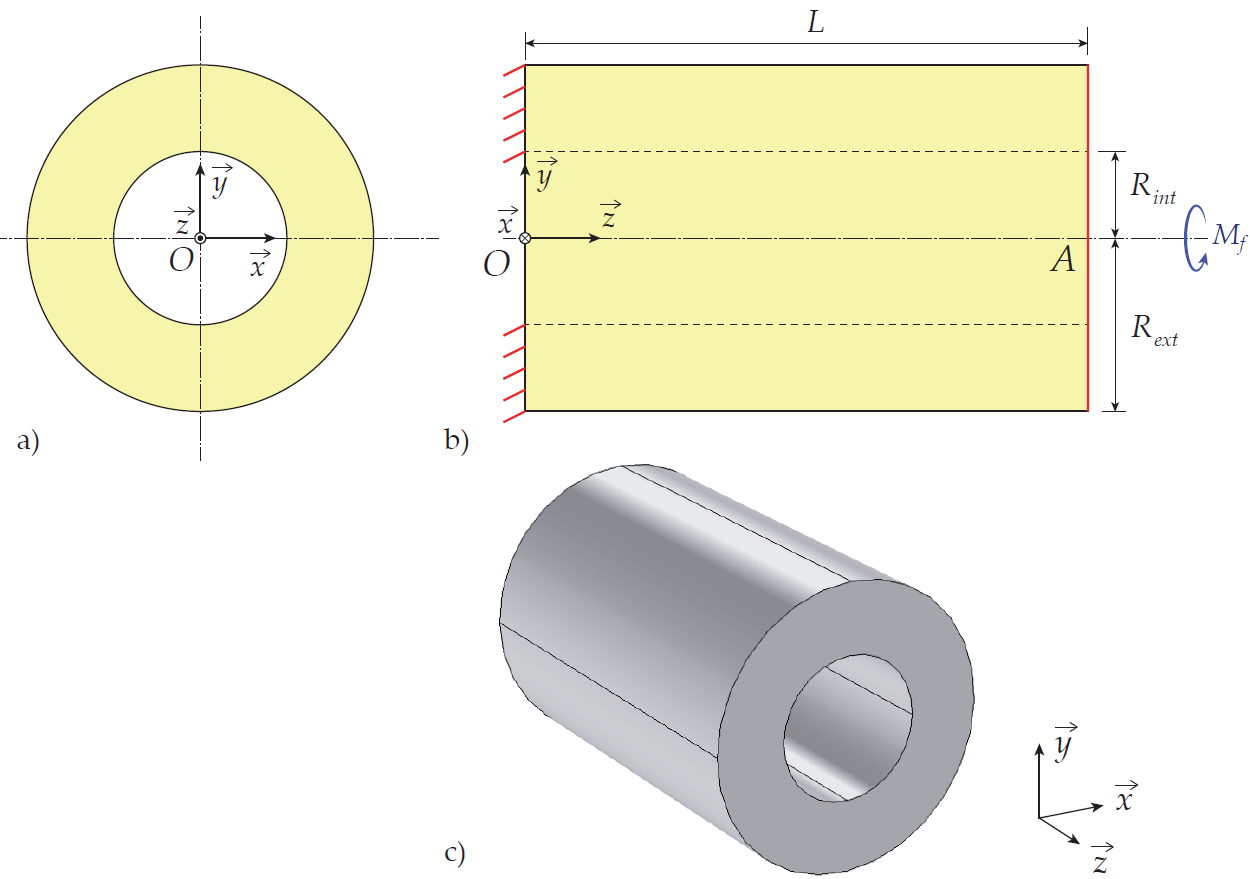
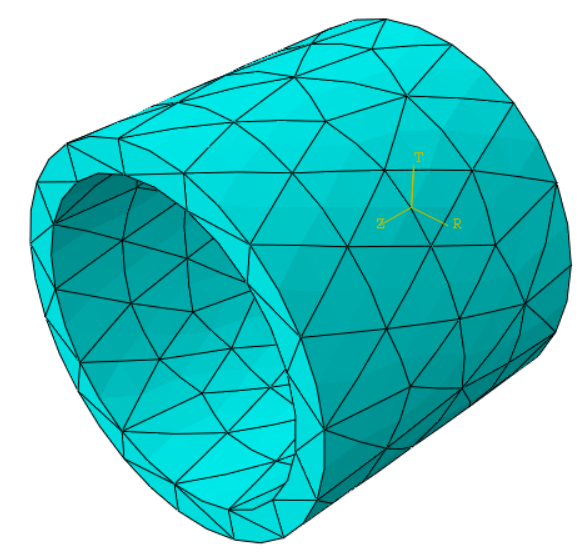
TP4 : Torsion La 4e séance de Travaux Pratiques est elle basée sur l’étude d’un cylindre creux sollicité en torsion.

La solution analytique de ce problème basée sur une étude tridimensionnelle de mécanique des milieux continus et servira de solution de référence pour l’étude. Dans Abaqus, un calcul numérique tridimensionnel sera effectué dans un premier temps, puis un calcul 1D utilisant des éléments Beam sera effectué.

Plaques et coques

Conditions aux limites avancées (2 séances)

Une difficulté souvent rencontrée dans la mise en donnée d’un problème éléments-finis est la définition précises des conditions aux limites s’appliquant sur le problème étudié. Parfois ces conditions aux limites se limitent à des équations assez simples : un déplacement ou des efforts appliqués sur une zone du domaine. Pendant les 2 séances de Travaux Pratiques consacrées à cette thématique, on apprendra à définir des conditions aux limites avancées pour des problèmes plus complexes au niveau de leurs frontières, notamment des problèmes avec contact et des problèmes de geométries périodiques.

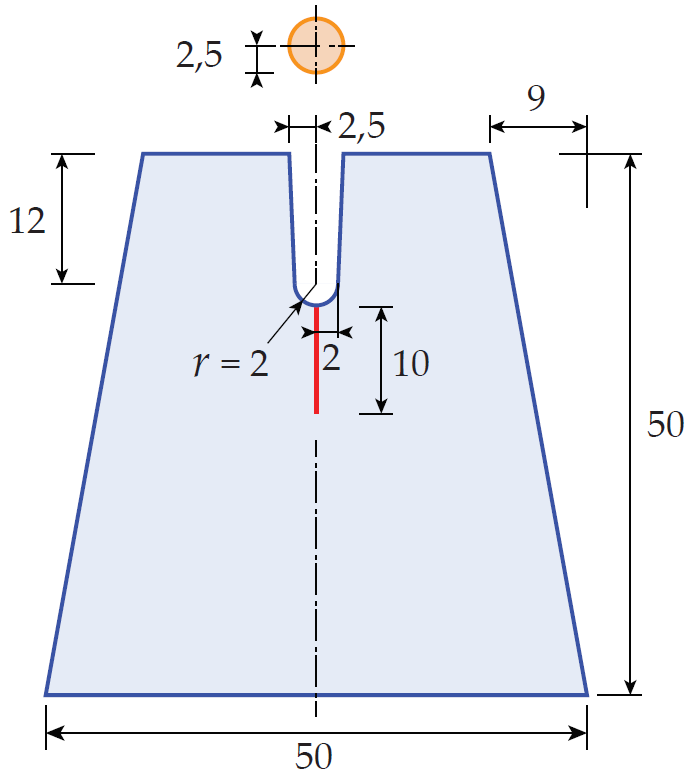
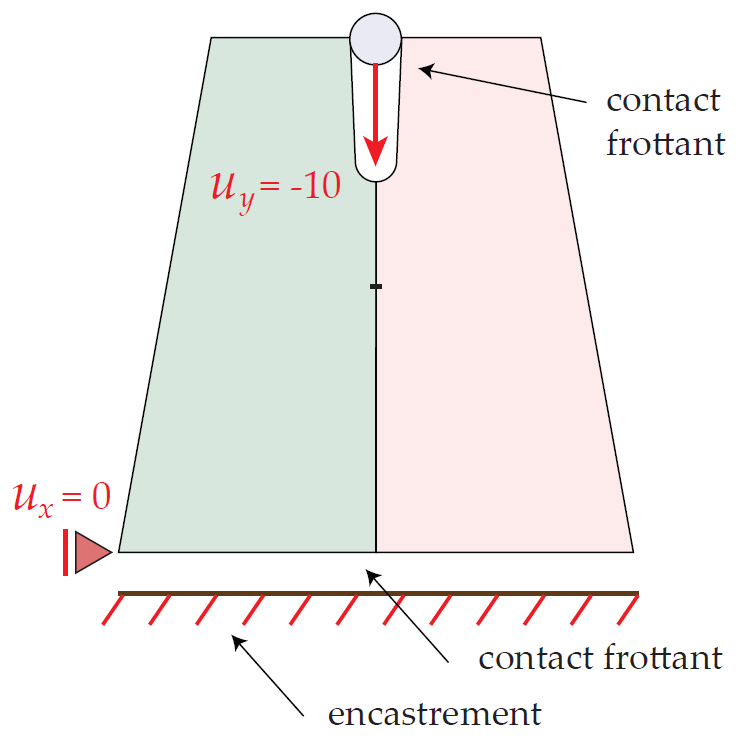
TP1 : Contact La 1e séance de TP permettra d’étudier du problème avec contact composé d’une éprouvette de forme trapèzoidale dans laquelle une encoche est creusée afin qu’un poinçon supposé rigide vienne s’y insérer.

Les bords de l’encoche étant inclinés, ceux-ci ont tendance à s’écarter lorsque le poinçon vient en contact ce qui a pour effet de rompre l’éprouvette lorsqu’un certain niveau de déformation est atteint. Pour cette séance de TP, on se place avant la rupture et on cherche à  simuler le problème du contact entre l’éprouvette déformable et le poinçon supposé rigide. Ce problème sera réutilisé plus tard pour l’étude de la fissuration. On suppose pour ce TP que sont connues la théorie du contact (notamment les équations de Kuhn-Tucker et le frottement de Coulomb) ainsi que les méthodes numériques de minimisation sous contraintes (notamment par pénalisation et multiplicateur de Lagrange). Dans Abaqus, différentes variantes de modélisation seront étudiées :

•  Le poinçon sera introduit dans le modèle sous la forme d’un Part de type Analytical Rigid ou Discrete Rigid.
• Le contact pourra être défini de type Node-to-Surface ou Surface-to-Surface avec un coefficient de frottement f égal à 0 ou 0,45.

Les courbes force-déplacement obtenues avec chacune des modélisations seront superposées et comparées.

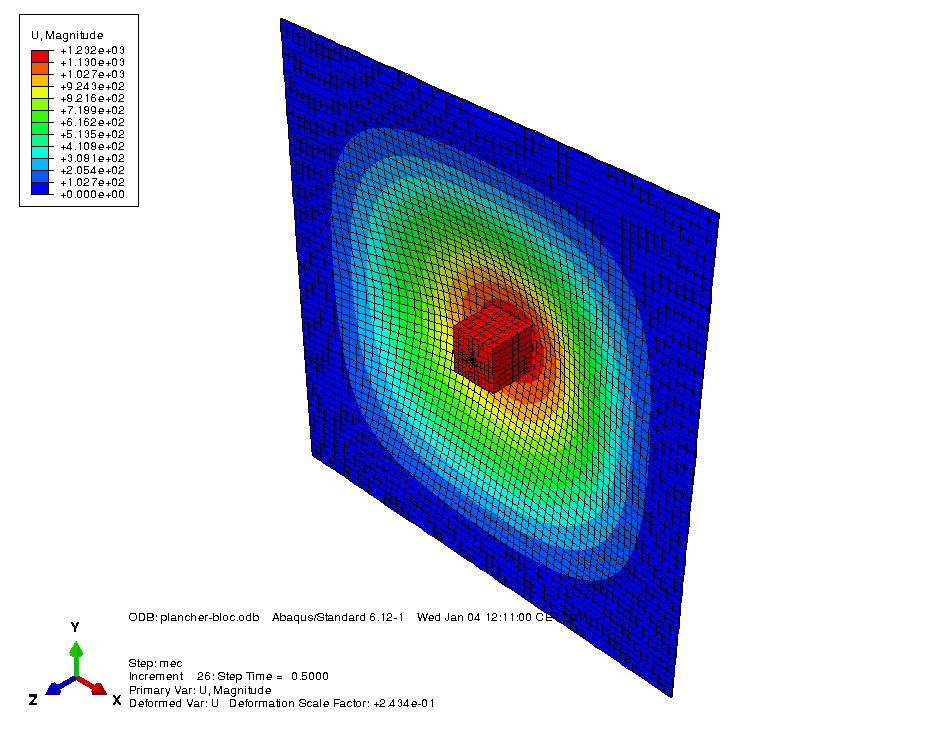
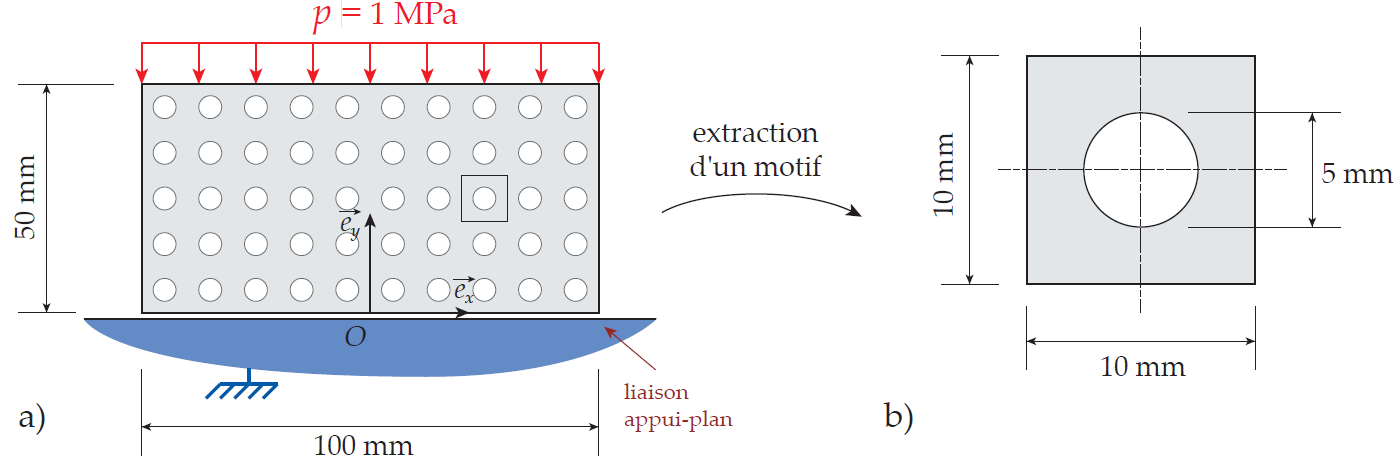
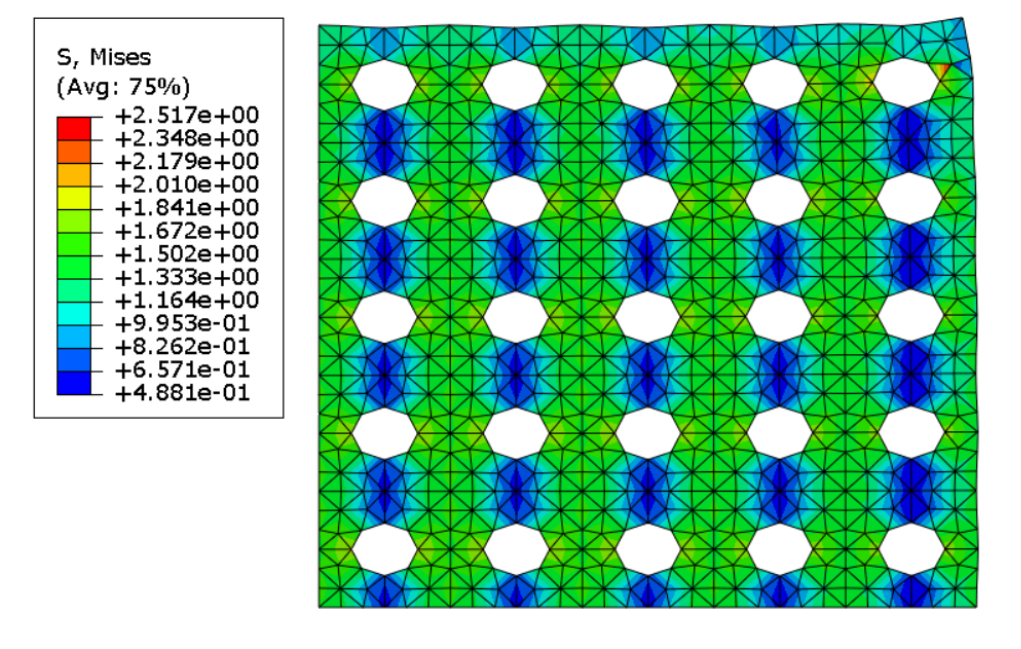
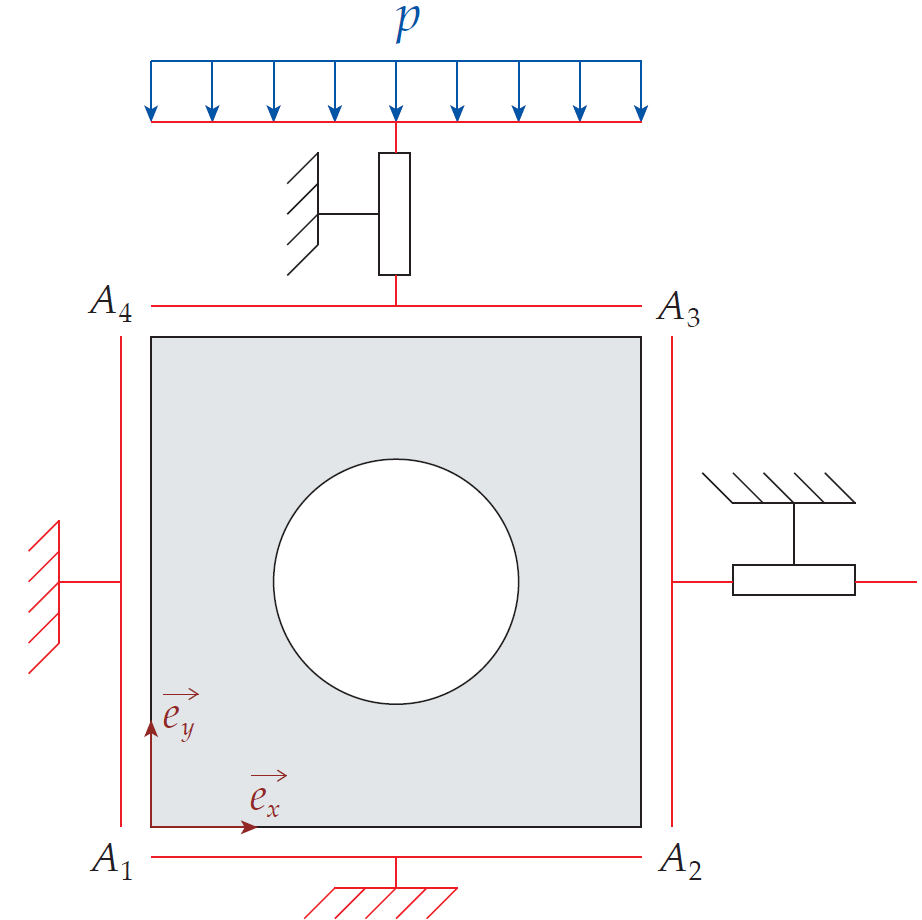
TP2 : Structure périodique La 2e séance de TP sera elle centrée sur l’étude d’une structure périodique, ce type de structure aillant des applications par exemple dans le domaine des matériaux composites. Cette structure est basée sur un motif (ici un carré comportant un trou circulaire en son centre) se répétant de nombreuses fois dans la structure. D’un point de vue numérique, la densité du maillage utilisé dépendra de la taille du motif se répétant dans la structure et si le nombre de motif total est important, le maillage comportera un très grand nombre d’élément ce qui peut remettre en question la faisabilité du calcul.

La réalisation d’un calcul sur l’ensemble de la structure montre que les motifs ne se trouvant pas sur le bord du domaine se déforment tous à peu près de la même manière.

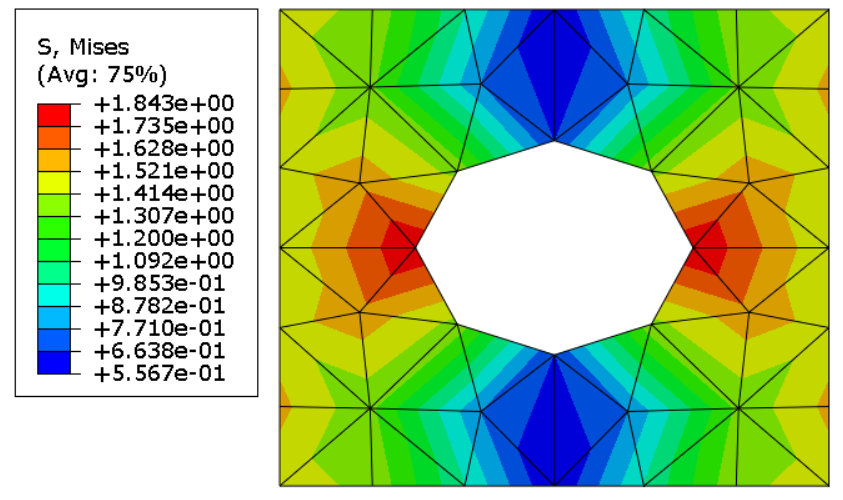
On peut donc en première approximation considérer que non seulement la géométrie du problème mais aussi sa solution est périodique. Dans ce TP on se propose donc de remplacer l’étude de la structure par l’étude d’un motif en cherchant a appliquer sur le motif les conditions aux limites permettant de reproduire le comportement d’un motif à l’intérieur de la structure.

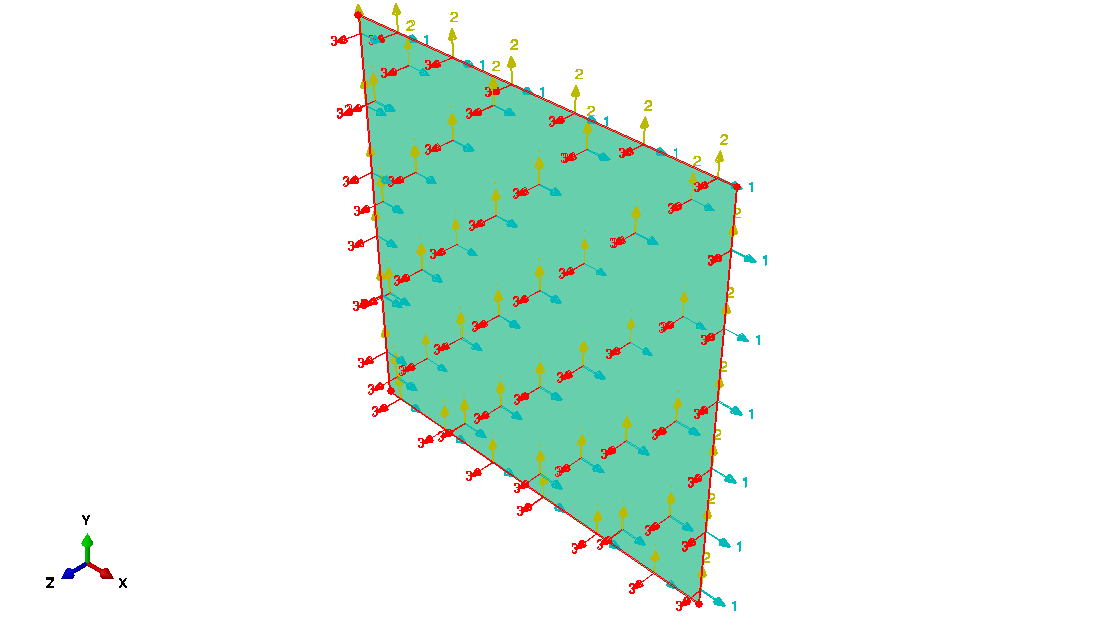
Pour appliquer ces conditions aux limites dans Abaqus, un Reference Point sera introduit dans le modèle dont les déplacements représenteront les allongements des bords droit et haut, puis une Equation sera ajoutée dans le modèle pour lier le déplacement de ces deux bord du domaine au déplacement du Reference Point.

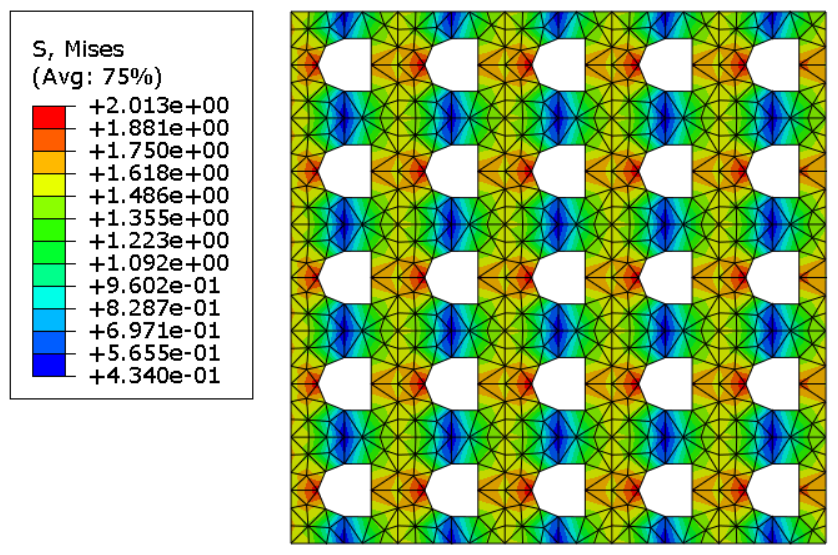
A la fin du TP, on s’intéressera à une structure dont le motif a une forme un peu plus complexe asymétrique.

Du fait de la perte de symétrie, la méthode employée précédement pour appliquer les conditions aux limites sur le bord d’un motif donnera des résultats approximatifs avec cette géométrie de motif. Pour aller plus loin dans l’étude des déformations de motifs périodiques il faudra s’intéresser au TP 3 “Homogénéisation”. 

TP3 (facultatif) : Homogénéisation Le dernier sujet de TP, ne faisant pas l’objet d’une séance attitrée en salle de TP informatique, permet d’aller plus loin dans la définition des conditions aux limites à appliquer sur un motif d’une structure périodique. Pour cela on utilise une toolbox gratuite pour Abaqus nommée Homtools permettant de définir trois type de conditions aux limites pour les motifs de structures périodiques. La plus précise de ces méthodes est celle correspondant à des conditions aux limites périodiques a appliquer sur les bords du domaine.

Plasticité (2 séances)

On cherche pour ses TP à reproduire dans Abaqus le comportement d’une éprouvette de traction lors d’un essai mécanique. Le point de départ sera les résultats d’un essai mécanique réalisé sur une éprouvette en acier dans une machine de traction. L’objectif des 2 séances de Travaux Pratiques et de réaliser des calculs numériques avec prise en compte des non-linéarités matérielles de telle sorte que les courbes force-déplacement pouvant être tracées se superposent avec les courbes expérimentales servant de référence. 

TP1 Pendant la 1e séance de TP, on trace la géométrie 2D dans une esquisse, on définit la partie élastique du comportement du matériau et les conditions aux limites afin d’effectuer un premier calcul élastique. Ce calcul élastique permet d’estimer de façon approximative une loi contrainte-déformation caractérisant le comportement du matériau. On utilise ensuite la loi contrainte-déformation ayant été obtenue comme donnée d’entrée d’un calcul élasto-plastique à mettre en donnée dans Abaqus.

TP2 Pendant la 2e séance de TP, on ajoute l’endommagement du matériau et la supression des éléments pour prendre en compte la rupture. De cette manière on peut à aller plus loin dans modélisation pour les grandes déformations, lorsque de le comportement du matériau devient adoucissant (lorsque la contrainte est une fonction décroissante de la déformation).

Endommagement

Dynamique

Rupture

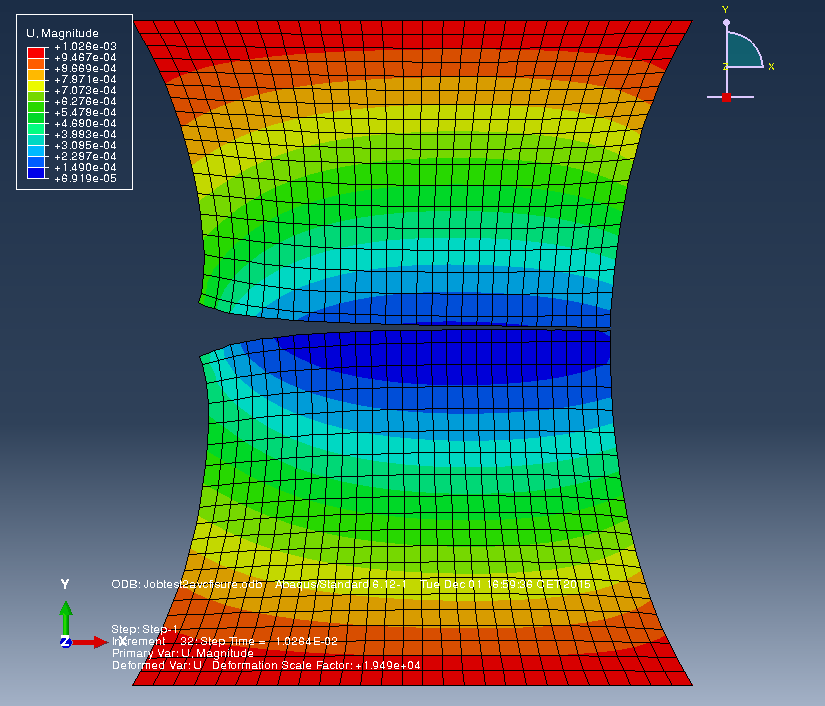
TP1 Le premier TP sur la rupture permet, sans se préoccuper de la propagation des fissures, de tester différentes pour introduire une fissure dans un matériau. On utilise d’abord la méthode Seam Crack qui permet d’introduire une fissure entre certains éléments composant le maillage. C’est cette méthode qui est utilisée pour obtenir le résultat de calcul présenté ci-dessous :

Cette méthode a l’avantage qu’il est possible d’effectuer numériquement un calcul d’intégrale J pour estimer le taux de restitution d’énergie élastique G. Ce calcul est effectué pendant le TP et on vérifie que l’on obtient bien un résultat proche de celui donné par la théorie pour une géométrie simple. Ce TP est aussi l’occasion de vérifier que le champ de déplacement donné par le logiciel correspond bien aux résultats théoriques prédit par les calculs de Westergaard (profil de fissure de forme parabolique) et de Williams (solution asymptotique de forme parabolique en pointe de fissure).

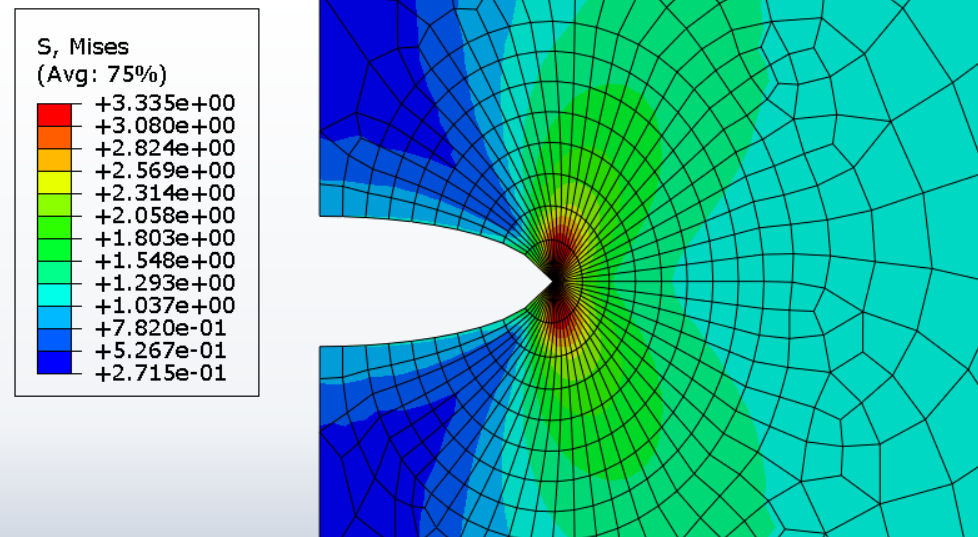
On teste ensuite une méthode alternative de maillage basée sur un maillage “radial” aboutissant au résultat montré ci-dessous :

Finalement, on teste une méthode alternative permettant d’introduire la fissure dans le maillage, nommée méthode X-FEM. Cette méthode permet de modifier les éléments-finis (fonctions de formes, intégration numérique) pour que la fissure puisse passer à travers les éléments-finis du maillage.

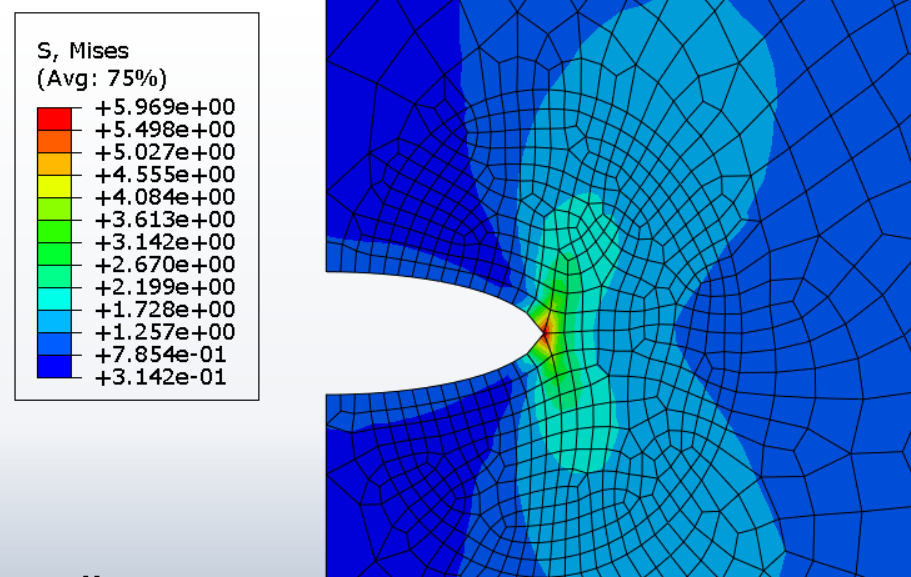
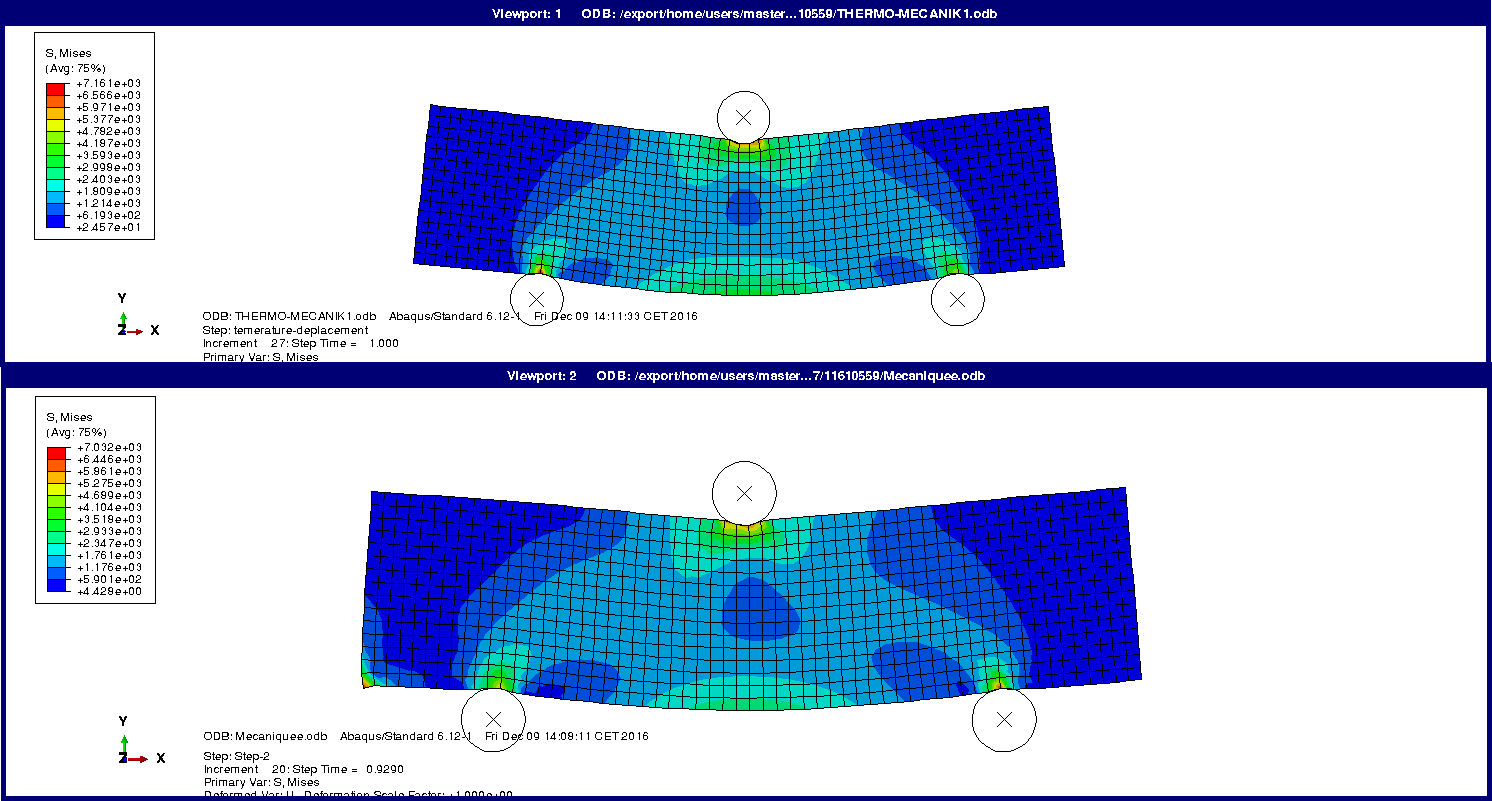
TP2 Dans la 2e séance de TP sur la mécanique de la rupture, on reprend la géométrie du cas test ayant été étudié dans la séance 1 des Travaux Pratiques sur les conditions aux limites avancées. On ajoute à l’éprouvette une préfissure permettant d’amorcer la fissuration du matériau. L’intérêt de ce cas test est d’étudier la fissuration de l’éprouvette avec une fissure se propageant verticalement de haut en bas à partir de l’extrémité de la pré-fissure.

Dans Abaqus, un maillage est réalisé de telle sorte que le trajet vertical connu de la fissure passe entre les éléments du maillage. Il n’y aura donc qu’a dédoubler les noeuds du maillage en appliquant correctement les conditions aux limites pour faire se propager la fissure. Dans un premier temps on fait se propager la fissure en utilisant la méthode “Virtual Crack Closure Technique”, conformément à la théorie énergétique de la rupture ou théorie de Griffith. On utilise ensuite une méthode alternative basée sur l’utilisation d’éléments cohésif.

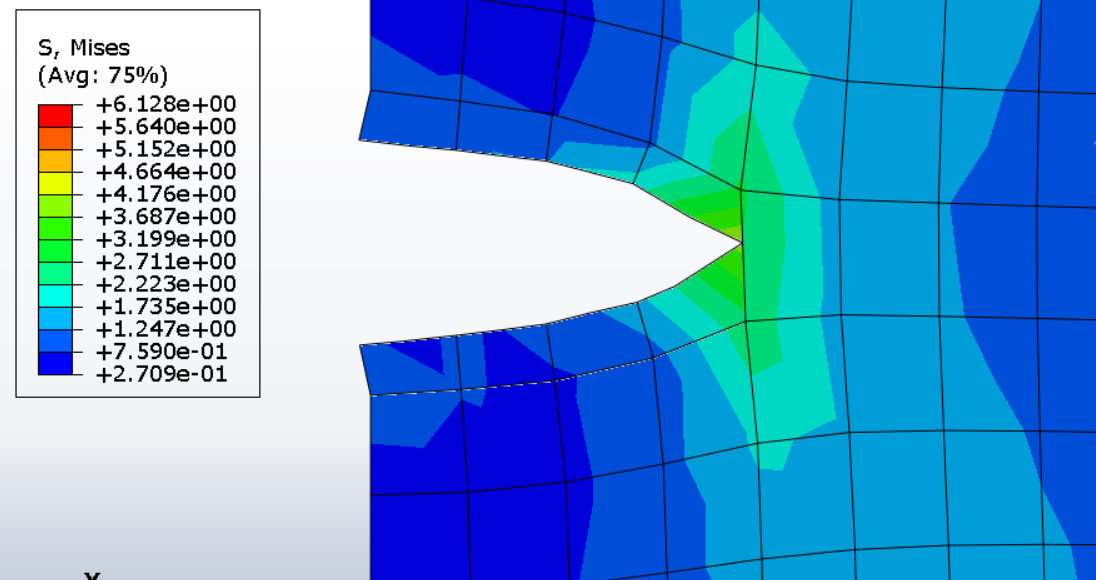
TP3 Dans la 3e séance de Travaux Pratiques, on reprend le même problème que dans la séance précédente, avec une fissure se propageant verticalement de haut en bas dans une éprouvette de forme trapézoïdale. La différence avec la séance précédente est que le maillage est réalisé de telle sorte que le trajet vertical de la fissure suivant le plan de symétrie de l’éprouvette passe à travers une bande d’éléments du maillage. Le problème de fissuration sera donc défini en utilisante la méthode des éléments-finis étendus (X-FEM).

Ici encore deux modèles de fissuration différents seront utilisés pour les calculs : d’abord le modèle de Griffith en utilisant la méthode VCCT utilisée dans Abaqus, ensuite un modèle cohésif. Pour définir le modèle cohésif on verra que deux méthodes sont possibles, l’une passant par modification du matériau et l’autre passant par la définition d’une loi d’interface.

Flambage

Vibration

Grandes déformations

Couches minces

a